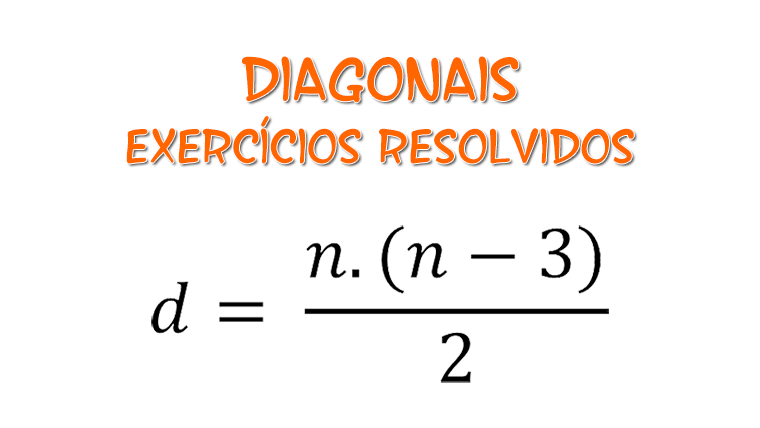No artigo anterior explicamos sobre as diagonais de um polígono e como chegar em sua fórmula.
Agora, vamos aplicar esta fórmula em alguns exercícios.
Pentágono (polígono de 5 lados):
d = n.(n-3)/2
d = 5(5-3)/2
d = 5.2/2
d = 10/2
d = 5 diagonais.
Ou seja, um pentágono tem 5 diagonais.
Heptágono (polígono de 7 lados):
d = n.(n-3)/2
d = 7.(7-3)/2
d = 7.4/2
d = 28/2
d = 14 diagonais.
Ou seja, um heptágono tem 14 diagonais.
Decágono (polígono de 10 lados):
d = n.(n-3)/2
d = 10.(10-3)/2
d = 10.7/2
d = 70/2
d = 35 diagonais.
Ou seja, um decágono tem 35 diagonais.
Dodecágono (polígono de 12 lados):
d = n.(n-3)/2
d = 12.(12-3)/2
d = 12.9/2
d = 108/2
d = 54 diagonais.
Ou seja, um dodecágono tem 54 diagonais.
Icoságono (polígono de 20 lados):
d = n.(n-3)/2
d = 20.(20-3)/2
d = 20.17/2
d = 340/2
d = 170 diagonais
Ou seja, um icoságono tem 170 diagonais.
Veja estes exercícios em vídeo clicando aqui.
Gostou? Compartilhe com os amigos!